Table of Contents
Class Prep
Class 1
Class 2
Class 3
Class 4
Class 5
Class 6
Class 7
Class 8
Class 9
Class 10
>>Topical Articles<<
Assumed Longitude
Bowditch
Bygrave
Casio fx-260 Solar II
Emergency Navigation
Making a Kamal
Noon Sight
Pub. 249 Vol. 1
Sextant Adjustment
Sextant Skills
Sight Averaging
Sight Planning,
Error Ellipses,
& Cocked Hats
Slide Rules
Standard Terminology
Star Chart
The Raft Book
Time
Worksheet Logic
BCOSA.ca
Performing sight reduction calculations in cramped, open cockpits with low temperatures and wind speeds of over 160 kilometers (100 miles) per hour was part of
what made navigation difficult in the early years of aviation. To address this challenge, Capt. L. C. Bygrave developed this slide rule shortly after World War 1.
It is, of course, a slide rule optimized for celestial navigation, and of limited use for general computations. For example, it would have been of little use to civil engineers, who were better off with the traditional 10 inch rule.

The advantage of a cylindrical slide rule is that you can replace the 10 inch wide scales of a straight slide rule with scales that were 480 inches wide, which gave improved accuracy in celestial navigation calculations. A modified version was used by Germany in World War 2 for navigation of their U-boats.
But these cylindrical slide rules were expensive to produce and they fell into disuse when Pub. 249 and Pub. 229 became available.
Many sets of equations have been developed over time to solve the celestial triangle. Captain Bygrave developed a set based on Napier's Rules of Circular Parts (around 1600 AD), which takes the navigational triangle and divides it into two right-angled spherical trianges. Doing this gives you formulas that only contain multiplications and divisions using cosines and tangents.
It is in the physical nature of slide rules that tangents involve scales that are twice as long as the sine/cosine scale. For instance, the tangent scale on a straight slide rule captures angles from 5.7° to 45° in 10 inches. It manages angles from 45° to 84.3° in a further 10 inches...for 20 inches in total.
In contrast, the sine scale on a straight slide rule squeezes all the angles from 5.7° to 90° into just 10 inches.
So — if you are doing the equations on a slide rule — the more your equations use tangent values rather than sine values, the more accurate your results are likely to be.
The Mark 1 Navigator's Slide Rule manages to stretch out tangent values to 40 inches of width...gaining still more accuracy in calculation compared to the conventional engineering slide rule. This cannot compete with the Bygrave cylindrical rule, with its 480 inches of scales...but it better than any other straight, 10 inch rule.
Indeed, every solution to the navigational triangle that has been developed over the past several centuries was optimized for the particular tools that were available at the time, and for the environment in which the solution was to be worked. The Bygrave equations are optimized for slide rules.
Understanding How the Bygrave Equations Work
I struggle here. I am like a cook who can follow a recipe to bake bread, but who does not understand the chemistry that goes into the interactions of the various ingredients in the dough. I was able to come up with this diagram from Ronand Van Riet's web page, but I still struggle with the derivation. Van Riet uses "X" as the solution to equation 1. In our worksheet, we use W for that value. Hence, I have slightly modified the diagram to use W as we use it.
Basically, I understand that this solution to the navigational triangle involves coming up with two right-angled spherical triangles, and then solving one of them. But this is as far as I can go.
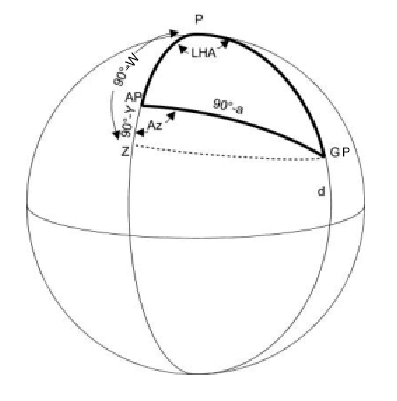
It looks to me like equation #2 from our worksheet...
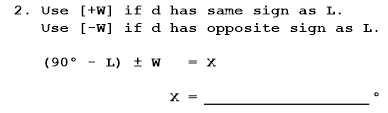
...is trying to sort out whether the two right angle spherical triangles we are going to solve look like this:
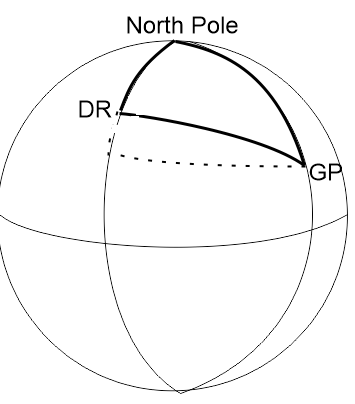
...or like this:
I am quite sure I have the shape of the second set of triangles wrong. I am still trying to visualize how these equations actually work. It ought to be possible to draw a graphic for each formula...but I cannot do that yet.
Sources:
https://en.wikipedia.org/wiki/Bygrave_slide_rule
https://www.nga.mil/About/History/TimeandNavigationExhibit/Pages/BygravePosition-LineSlideRule.aspx
https://www.sliderulemuseum.com/Papers/PositionLineSlideRules_RonaldWMvanRiet.pdf