Table of Contents
Class Prep
Class 1
Class 2
Class 3
Class 4
Class 5
Class 6
Class 7
Class 8
Class 9
Class 10
>>Topical Articles<<
Assumed Longitude
Bowditch
Bygrave
Casio fx-260 Solar II
Emergency Navigation
Making a Kamal
Noon Sight
Pub. 249 Vol. 1
Sextant Adjustment
Sextant Skills
Sight Averaging
Sight Planning,
Error Ellipses,
& Cocked Hats
Slide Rules
Standard Terminology
Star Chart
The Raft Book
Time
Worksheet Logic
BCOSA.ca
And for those who are REALLY hooked on navigation without batteries...
Sight Reduction by Slide RuleProcedures to use a slide rule are a bit complex because there are different types of slide rule, and the "how" varies from one type to another. I
think of them as being in four overall categories.
"Trig not possible" slide rules An example of this would be the Aristo-Junior. It does not have an S or T scale. "Trig is Possible" slide rules The Thornton AA-010 rule includes the S, T and ST scales, but has them on the body of the rule. You cannot use trig values directly in a formula if the scales are not on the slide. However, you can determine the trig value of any angle in range, and write it down
on paper. Then you can perform your calculations using the C and D scales. When you get your answer for a given equation, you position your cursor over the value on the D
(or in the case of tangent values for angles above 45°, on the DI scale) and then read the value in degrees from the trig scales on the body of the rule. "Optimized for Trig" slide rules Has S and T scales only The Raven has S and T scales on the slide. Sines and cosines are both handled on the S scale...with sine values printed in black ink, and cosines in red ink. Tangents are handled on the T scale, with
values from 5° to 45° printed in black (and read on the C scale) and values from 45° to 85° printed in red (and read on the CI scale
from the reverse of the rule). Has S, T and ST scales The Hemi Versalog rule includes the SRT scale (which most slide rules call, simply, the ST scale), which allows for sines and tangents down
to 0.6° and cosines up to 89.4°. Small-angles sines and tangents have identical values (to "slide rule accuracy") and are both handled on the ST scale. Large angle cosines, above 85°,
are also handled on this scale, and are printed in red. As with the Raven, the tangents from 45° to 85° are read on the CI scale (on the reverse of the rule) rather than the C scale. The Mark 1 Navigator's Slide Rule The Mark 1 omits a number of common slide rule scales (e.g. the LL scales), and has been optimized for trig. Further, in that navigators typically
work in degrees and minutes, the Mark 1 allows users to skip the step of converting angles into decimal degrees. The tangent scales all move from left to right, which eliminates the need for using inverted C or D scales to read the results (i.e. the CI or DI scale). Cosines are still read from right-to-left on the S and ST scales. All of the Bygrave equations for sight reduction yield results that are tangents. By putting a full array of tangent scales on the body, as well as the slide,
results can be read directly as angles, rather than being read as values on the D scale, which are then converted into angles in a separate step. These features... You may download the entire User Guide for this slide rule
by clicking here. But the section below will give you a feel for how the Mark 1
handles trig formulas.
Click here for an online emulator of the Mark 1 rule. (The emulator works only on
a conventional computer with a mouse. It will not work with any sort of touchscreen.)
Comparing Three Slide Rules in Solving a Problem The first formula in the Bygrave equations for sight reduction is:
tan(d) ÷ cos(t) = tan(W)
where d = the declination of the celestial object, and t = the meridian angle. Assuming that d = 44° 19.7' and t = 30°49.2', here are the steps to solve the equation.
Accuracy of Slide Rule Sight Reduction Paul Hirose performed a statistical analysis of slide rule accuracy in calculating the Bygrave equations, and found that the average
Hc accuracy was within 1.8', with 95% correct to within 3.7'.
The standard I use for navigational significance is "Can I find Bermuda using my celestial navigation techniques?"
The highest point in Bermuda is 260 feet above sea level. From a small yacht, you will see Bermuda on the horizon as long as you are no further than 20 nm away. In a pre-GPS era, more than one sailor simply missed Bermuda, and sailed on to Europe without ever
seeing this small island group.
If you have a sextant error of 4 nm, and a slide rule, sight-reduction error of 1.3 nm, you will have no trouble finding Bermuda. So then, I would say that a slide rule error of 1.3 nm is not navigationally significant.
If you are sailing in the Pacific and navigating between volcanic islands, then celestial navigation is even more forgiving. The highest point in Tahiti is 7,352 feet above sea level. You absolutely cannot miss it as long as you have even the remotest idea of what you are doing with your sextant and slide rule.
As soon as you make a landfall, you will put your sextant back in its box and begin to use piloting techniques, including hand-bearing compass, depth sounder, and radar, to guide you into port.


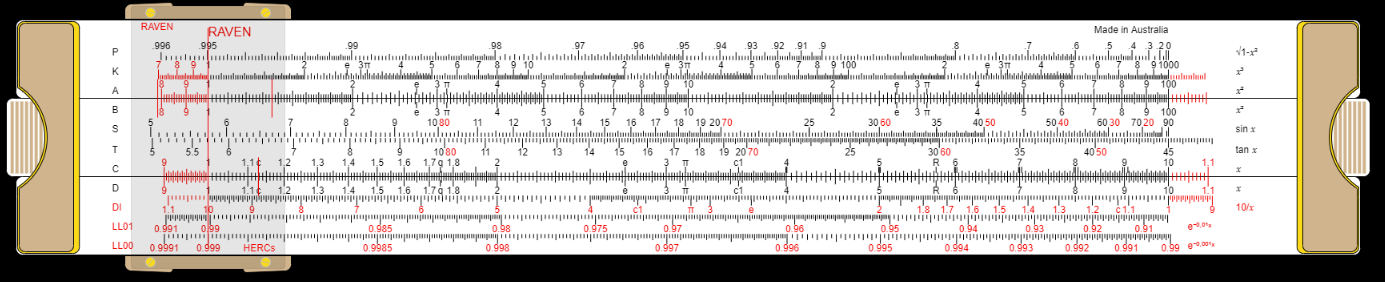
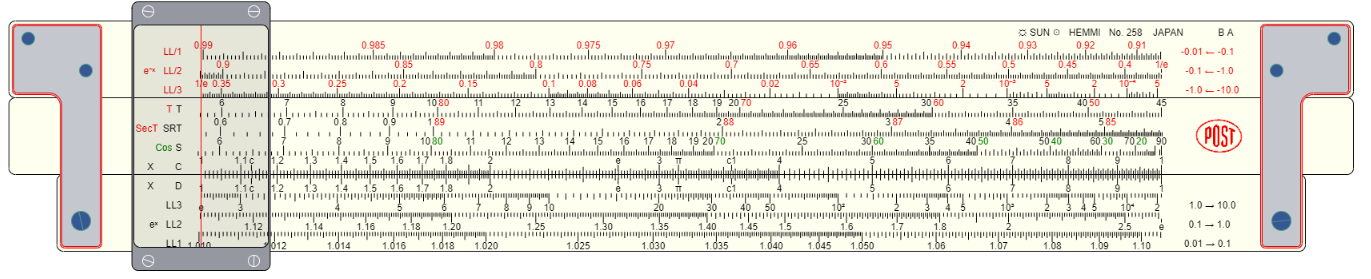

...make it possible to complete sight reduction and great circle calculations with a Mark 1 faster than with a general purpose trig rule such as the Hemi Versalog.
"Trig is Possible"
14 Steps
"Optimized for Trig"
11 Steps
"Optimized for Navigational Trig"
3 Steps
You know at a glance that 0.9 ÷ 0.8 is greater than 1, so you know that this tangent value is going to be greater
than 45°. You also know that to convert tangent values back into degrees, you need to use the DI scale. So...
Make a mental note that tan(44°) is roughly 0.9.
You know at a glance that 0.9 ÷ 0.8 is slightly greater than 1, so you know that this tangent value is going to be greater
than 45°. You also know that to convert tangent values back into degrees, you need to use the DI scale. So...
Make a mental note that the value of tan(44°) is roughly 0.9.
(With slide rule accuracy, it is difficult
precise with a cosine in this range.)
Make a mental note, by looking at the C scale value beneath tan(30° 50') is roughly 0.8.