Table of Contents
Class Prep
Class 1
Class 2
Class 3
Class 4
Class 5
Class 6
Class 7
Class 8
Class 9
Class 10
>>Topical Articles<<
Assumed Longitude
Bowditch
Bygrave
Casio fx-260 Solar II
Emergency Navigation
Making a Kamal
Noon Sight
Pub. 249 Vol. 1
Sextant Adjustment
Sextant Skills
Sight Averaging
Sight Planning,
Error Ellipses,
& Cocked Hats
Slide Rules
Standard Terminology
Star Chart
The Raft Book
Time
Worksheet Logic
BCOSA.ca
To understand this discussion of the worksheet, you must of course HAVE a worksheet to look at. Download the sight reduction worksheet from here.
Basic Questions
- What time is it?
- Where do I think I am? (You don't know for sure...which is why you are trying to get a fix. But you have a rough idea of where you are, within a few dozen miles.)
- What does my sextant tell me?
Enter this information in the first three sections of the form.
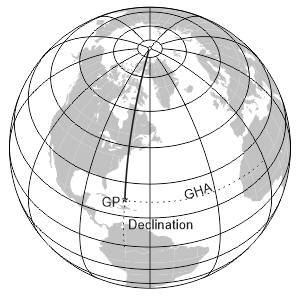
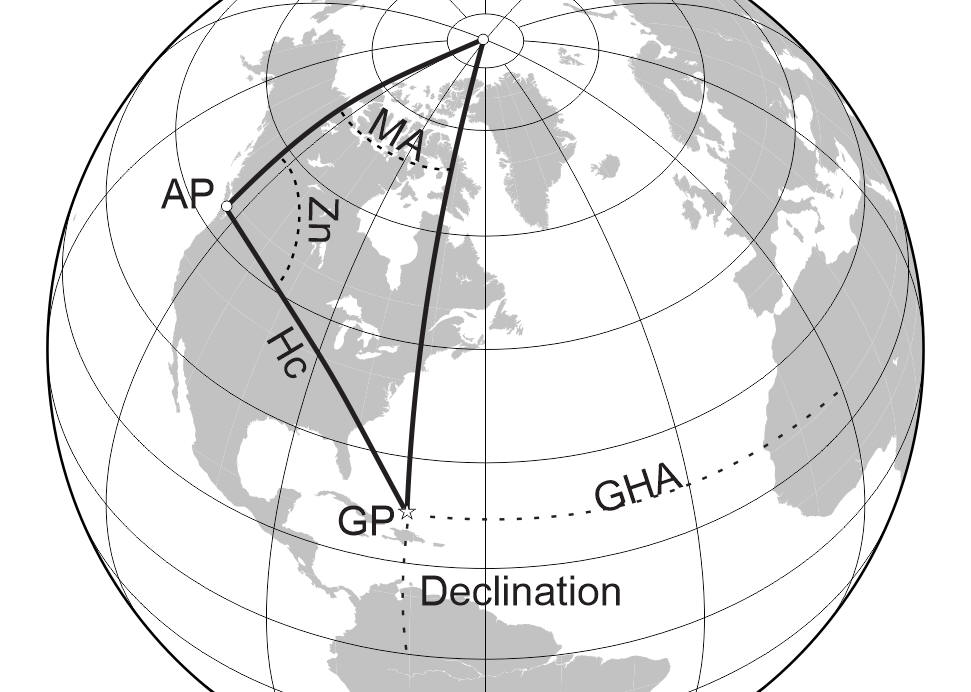
Where is the GP?
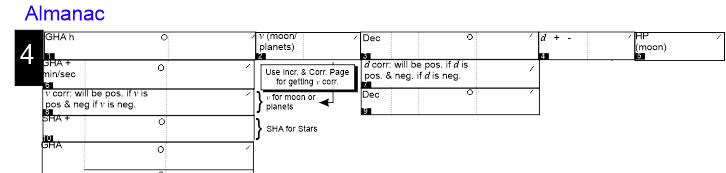
The next task you have to do is to figure out where the GP (geographical position) of your celestial object is. This is the point where the sun (or whatever celestial object you have selected) is directly overhead.
You will get this information from the Nautical Almanac. It allows you to determine the GP of a celestial object for any day of the year, down to the precise hour and second.
You now have the first side of your navigational triangle: a line drawn from the North Pole to the GP.
Where am I, revisited?
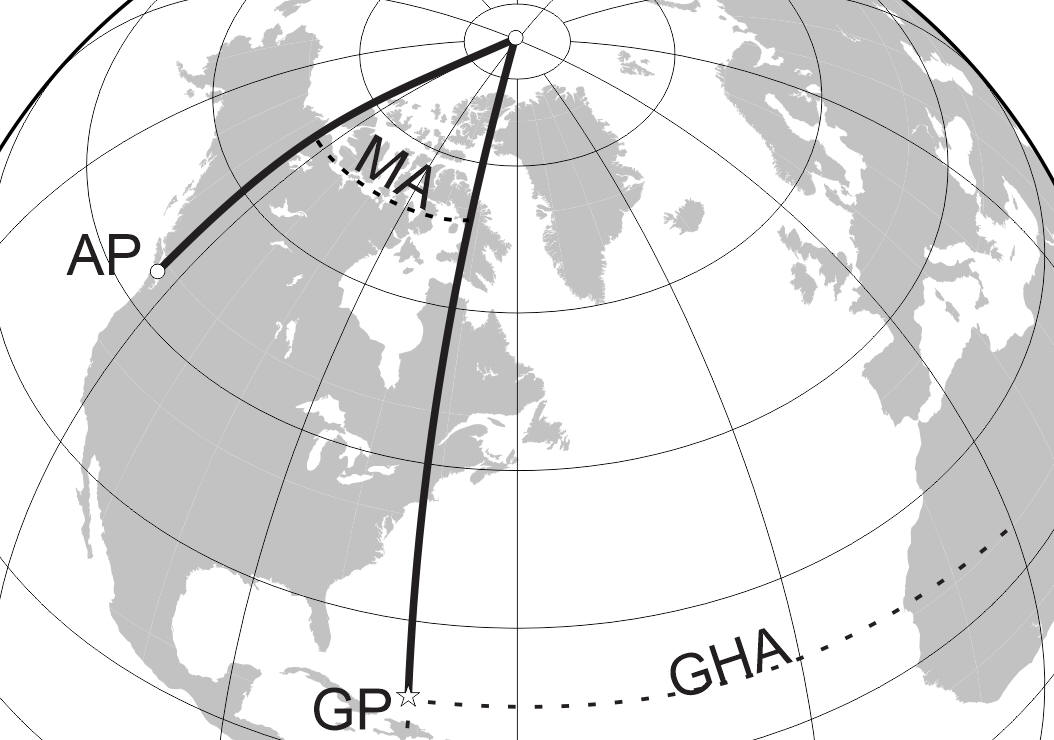
We will refine your DR postion into an AP (assumed position). It is within a few miles of your DR, and is chosen to make the subsequent calculations easier to do. You could work out a fix using only your DR position. Just trust me for now that creating a fictional assumed position, which is close to your DR, really does make it easier in the end.
Once you have your assumed position, you have two sides of your navigational triangle.
Once you get the included angle between these two lines, you can use mathematics to work out the length and angle of the missing side. But to keep the math manageable, it is helpful to deal in whole degrees, rather than fractions of a degree. This angle is called the Meridian Angle (confusingly abbreviated by a t, or by MA, or by LHA - for "Local Hour Angle").
You now know everything you need to know, mathematically speaking, to describe the third side of your triangle. You can do this with a hand calculator, using sines and cosines, in about 4 minutes.
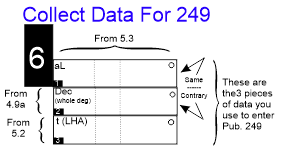
OR...you can go to Pub. 249, Sight Reduction Tables, which contain solutions for every possible navigational triangle. This process takes only 1 minute...so most navigators choose to use Pub. 249 rather than using a hand calculator.
Calculate the Final Side of the Triangle
To make the next step easy, you take a moment to collect all the little bits of information you will need to make use of Pub. 249.
Thense Section 7 of the worksheet to do this.
In the end, you will get an Hc, usually called "Height Calculated"...though you could equally well call it a "Hypothetical Calculation". For if your vessel WAS precisely at the AP, this is EXACTLY what your sextant reading would be. This also tells you the bearing of the celestial object from you (abbreviated as Z and called the azimuth angle; this will be converted into Zn, the azimuth, which is precisely the same as the compass bearing from your vessel to the object).
Naturally, though, you are not at the AP. You are somewhere else. You want to find out where that somewhere else is.
First, though, you are pretty sure that your azimuth is the same as what you calculated. You could be scores of miles off in your DR, and your azimuth would still be the same. It is a big earth, and azimuth doesn't change quickly.
You may wonder why we go to the effort of calculating an azimuth, rather than just pointing a hand compass at the sun. The truth is that the human eye is unable to find the center of the sun with any great accuracy. The brightness throws us off. Further, a hand bearing compass works best getting the azimuth of things like lighthouses, which lie along the horizon. We simply cannot use a hand compass to get an adequate bearing of an object that is 45° high in the sky.
We get more accuracy by using the Nautical Almanac plus Pub. 249 and calculating the azimuth.
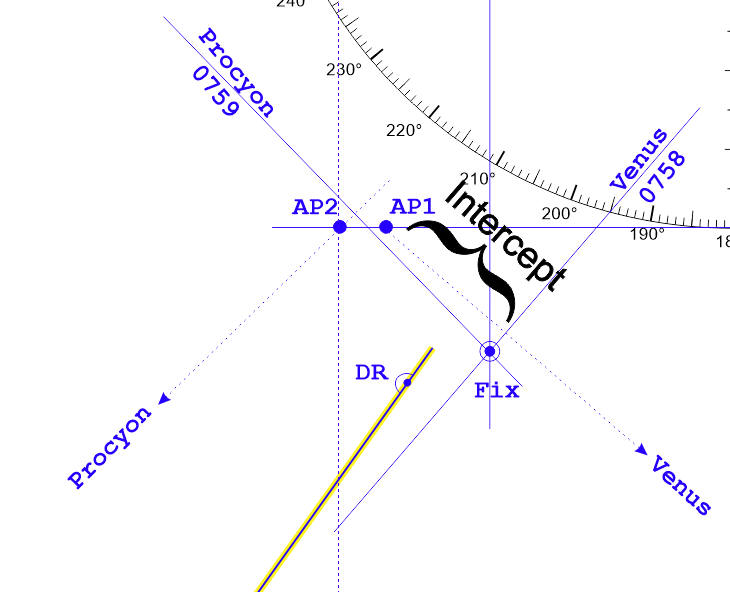
Getting from an AP to a FIX
We use Section 7 of the worksheet, to apply a few final corrections to our sextant data, and then to relate the height of the object as read by the sextant (called Hs, or Height Sextant) to the Hc.
We then work out our distance and direction from the AP, and then we know where we are. In this example, you will see that we have used two celestial objects - one star and one planet - and are able to work up a fix of where we really are.
.